Stochastic Fountain Dynamics
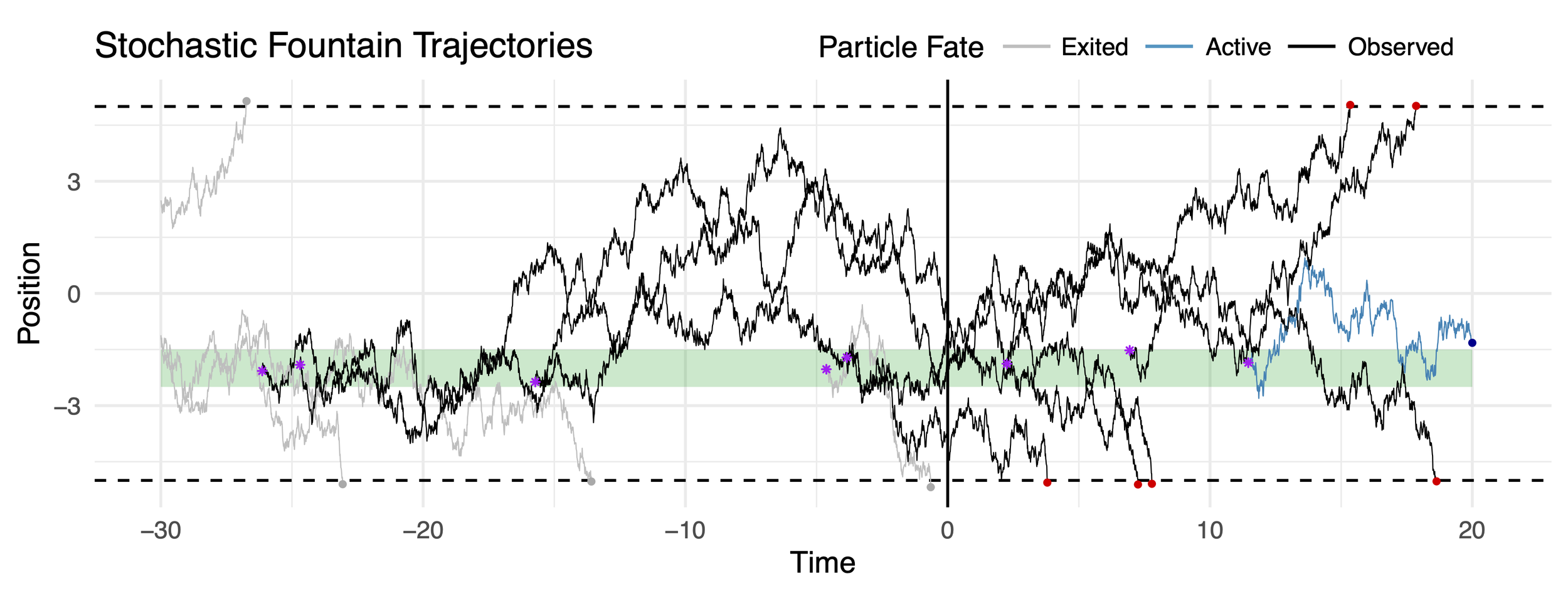
In the last couple of years, I have noticed an emerging theme in my work. Across multiple biological systems, colleagues and I have articulated models that involve particles that (1) emerge at random times from a fixed source-location distribution; (2) move throughout a local environment randomly (either diffusing, or switching between deterministic states); and (3) are removed from the system due to state-switching or escape from some predefined region.
I am tentatively calling these systems “stochastic fountains.”
What do these stochastic fountains look like when you only have access to partial information. For example, what if you only have a snapshot of particles at one instant in time? Or, what happens if you can only observe particles at the moment they leave the domain? The associated inference problems arise naturally in mathematical biology applications, and are a fascinating example of how statistical (Fisher) information can be used to assess the quality of data in partially observed systems.
Often live-cell single particle tracking techniques only capture a brief window into a cell’s spatial distribution of particles. Can we still learn parameters of particle dynamics anyway?
Inferring dynamics from snapshots
Inferring Stochastic Rates from Heterogeneous Snapshots of Particle Positions. Christopher E Miles, Scott A McKinley, Fangyuan Ding, Richard B Lehoucq. Bulletin of Mathematical Biology. Vol 86, No 74, pgs 1-31. (2024) ( pdf )
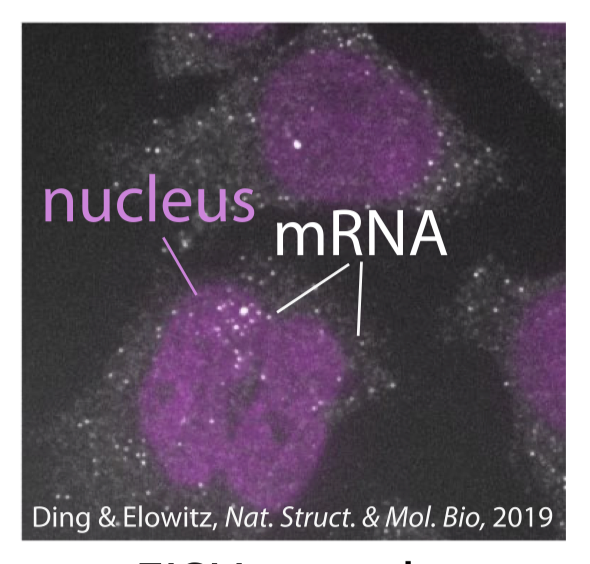
Many imaging techniques for biological systems—like fixation of cells coupled with fluorescence microscopy—provide sharp spatial resolution in reporting locations of individuals at a single moment in time but also destroy the dynamics they intend to capture. These snapshot observations contain no information about individual trajectories, but still encode information about movement and demographic dynamics, especially when combined with a well-motivated biophysical model. The relationship between spatially evolving populations and single-moment representations of their collective locations is well-established with partial differential equations (PDEs) and their inverse problems. However, experimental data is commonly a set of locations whose number is insufficient to approximate a continuous-in-space PDE solution. Here, motivated by popular subcellular imaging data of gene expression, we embrace the stochastic nature of the data and investigate the mathematical foundations of parametrically inferring demographic rates from snapshots of particles undergoing birth, diffusion, and death in a nuclear or cellular domain.
Toward inference, we rigorously derive a connection between individual particle paths and their presentation as a Poisson spatial process. Using this framework, we investigate the properties of the resulting inverse problem and study factors that affect quality of inference. One pervasive feature of this experimental regime is the presence of cell-to-cell heterogeneity. Rather than being a hindrance, we show that cell-to-cell geometric heterogeneity can increase the quality of inference on dynamics for certain parameter regimes. Altogether, the results serve as a basis for more detailed investigations of subcellular spatial patterns of RNA molecules and other stochastically evolving populations that can only be observed for single instants in their time evolution.
Stochastic gradient descent where the gradients are computed through Monte Carlo simulation of the model’s generating paths.
Inferring a source from boundary exits
Source identification via pathwise gradient estimation.
Richard B. Lehoucq, Scott A. McKinley, Petr Plecháč. arXiv2505.18205
Submitted and under review, 2025. ( pdf )
In the context of PDE-constrained optimization theory, source identification problems traditionally entail particles emerging from an unknown source distribution inside a domain, moving according to a prescribed stochastic process, e.g.~Brownian motion, and then exiting through the boundary of a compact domain. Given information about the flux of particles through the boundary of the domain, the challenge is to infer as much as possible about the source.
In the PDE setting, it is usually assumed that the flux can be observed without error and at all points on the boundary. Here we consider a different, more statistical presentation of the problem, in which the data has the form of discrete counts of particles arriving at a set of disjoint detectors whose union is a strict subset of the boundary. In keeping with the primacy of the stochastic processes in the generation of the model, we present a stochastic gradient descent algorithm in which exit rates and parameter sensitivities are computed by simulations of particle paths. We present examples for both Itô diffusion and piecewise-deterministic Markov processes, noting that the form of the sensitivities depends only on the parameterization of the source distribution and is universal among a large class of Markov processes.