Viscoelastic Diffusion and the Generalized Langevin Equation
The last twenty years have seen a revolution in tracking data of biological agents across an impressive range of spatial and temporal scales. An important and ubiquitous observation from these studies is that path trajectories of living organisms are often poorly described by the classical model for random movement in continuous time, Brownian motion.
To abuse a sentiment from Tolstoy: Brownian diffusions are all alike, but every anomalous diffusion is anomalous in its own way. In the details of the non-Brownian statistics lie vital clues to fundamental physical and physiological mechanisms of transport and interaction in living systems. The primary focus of my research in Applied Stochastic Processes has been to work directly with bioengineers and ecologists to determine the implications of anomalous diffusive data for both small scale physiology and for large scale animal population dynamics.
Analysis of a model for Gaussian subdiffusion
Anomalous Diffusion and the Generalized Langevin Equation ( pdf )
Scott A McKinley and Hung D Nguyen, SIAM Journal on Mathematical Analysis. Vol 50, No 5, pgs 5119-5160. (2018)
The generalized Langevin equation (GLE) is a stochastic integro-differential equation that is commonly used to describe the velocity of microparticles that move randomly in viscoelastic fluids. Such particles commonly exhibit what is known as anomalous subdiffusion, which is to say that their position mean-squared displacement (MSD) scales sublinearly with time. While it is common in the literature to observe that there is a relationship between the MSD and the memory structure of the GLE, and that there exist special cases where explicit solutions exist, this connection has never been fully characterized. Here, we establish a class of memory kernels for which the GLE is well-defined, we investigate the associated regularity properties of solutions, and we prove that large-time asymptotic behavior of the particle MSD is entirely determined by the tail behavior of the GLE’s memory kernel.
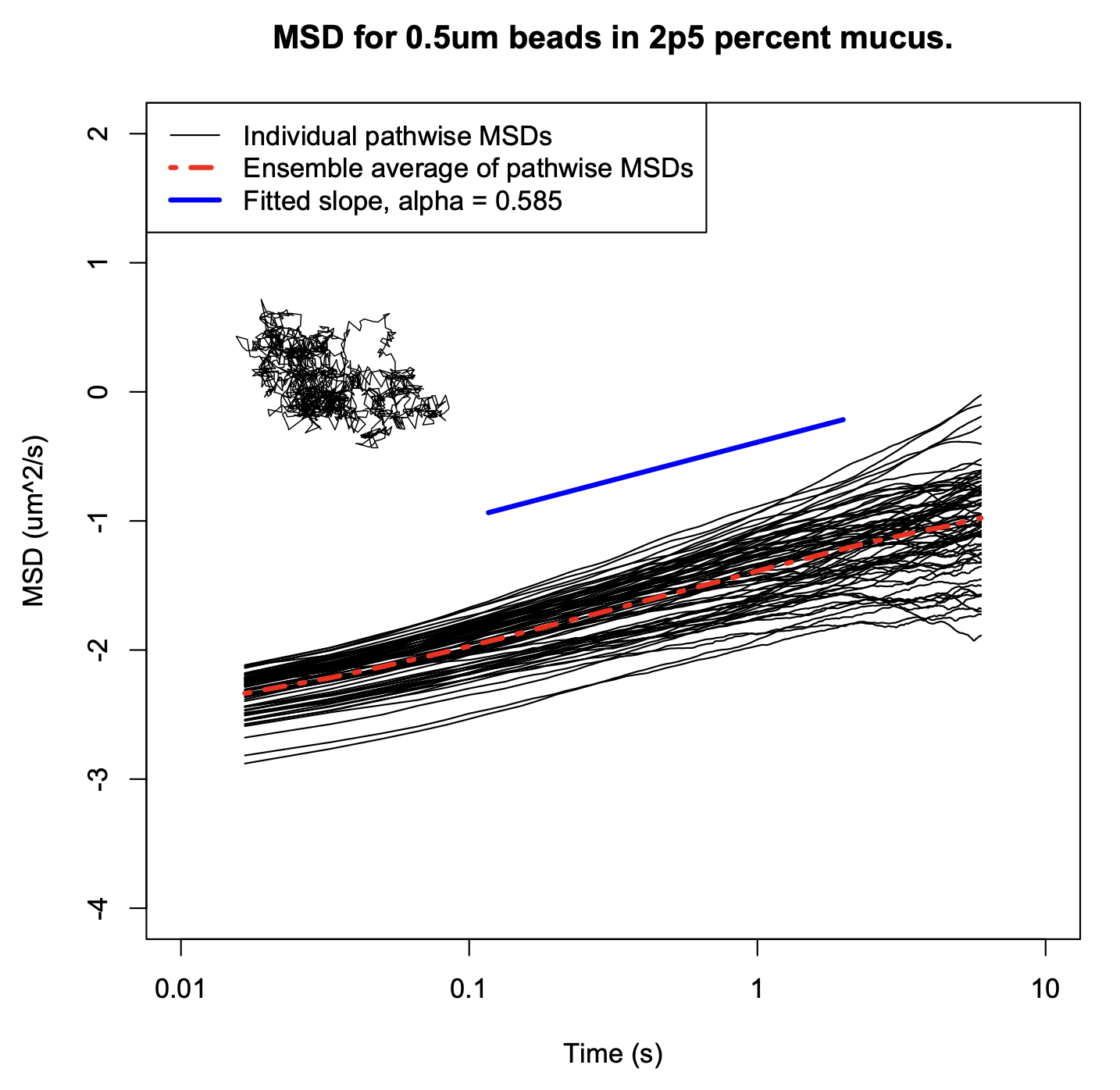
Pathwise Mean-Squared Displacement data from Hill et al (2014). The variance of Brownian motion grows linearly in time, but data collected from particles fluctuating in viscoelastic fluids regularly displays sublinear growth. When coupled with the observation that consecutive displacement increments are anti-correlated, this builds a case for using the GLE to model this motion.
Using particle movement to learn about fluid environments
Reconstructing Complex Fluid Properties from the Behavior of Fluctuating Immersed Particles. ( pdf ) with Christel Hohenegger.
SIAM Journal on Applied Mathematics. Vol 78 No 4, pgs 2200-2226 (2018)
Complex fluids have long been characterized by two functions that summarize the fluid's elastic and viscous properties, respectively called the storage G’(ω) and loss G’’(ω) moduli. A fundamental observation in this field, which is called passive microrheology, is that information about these bulk fluid properties can be inferred from the path statistics of immersed, fluctuating microparticles. In this work, we perform a systematic study of the multistep protocol that forms the foundation of this field. Particle velocities are assumed to be well described by the Generalized Langevin Equation, a stochastic integro-differential equation uniquely characterized by a memory kernel, which is hypothesized to be inherited from the surrounding fluid. In this work with Christel Hohenegger (Utah), we investigate the covariation between a particle's velocity process and the non-Markovian fluctuations that force it, and we establish rigorous justification for a key relationship between a particle's Mean Squared Displacement and its memory kernel. With this foundation in hand, by way of a tunable four-parameter family of functions that can serve as particle memory functions, we analyze errors and uncertainties intrinsic in passive microrheology techniques. We show that, despite the fact that certain parameters are essentially unidentifiable on their own, the protocol is remarkably effective in reconstructing G’(ω) and G’’(ω) in a range that corresponds to the experimentally observable regime.
A range of statistically plausible storage and loss moduli inferred from single particle tracking data in a viscoelastic fluid.